Its main purpose is to summarise and describe essential features of a dataset. Descriptive statistics are crucial for simplifying large amounts of data and making it more understandable.

Definition: Mean is also known as the average. Mean is the sum of all values in a dataset divided by the number of observations

Formula: $\overline{x}=\frac{\sum x_i}{n}$

Use-Case: It is suitable for symmetrically distributed data without extreme outliers and and when each data point contributes equally to the central value.

Definition: Median is a measure of central tendency that represents the middle value in a dataset when it is arranged in ascending or descending order.

Formula:

• Odd Number of Samples: $\frac{n+1}{2}$
• Even Number of Samples: $\frac{\frac{n}{2}+(\frac{n}{2}+1)}{2}$ (To split in the middle)

Use-Case: It is useful where the datasets contains extreme outliers or when the distribution is skewed. It provides a more robust measure of central tendency compared to the mean.

Definition: The mode is a measure of central tendency that represents the most frequently occurring value(s) in a dataset.

Formula: Select the value(s) with the highest frequency of occurrence.

Use-Case: It is useful for analysing categorical data, such as colours, types, or categories, where identifying the most common value is meaningful.

The difference between the maximum and minimum values in a dataset.

IQR provides information about the spread of the dataset. It is based on quartiles, which divides a dataset into 4 equal segments.

1. Calculate Quartiles:
   • Arrange the dataset in ascending order.
   • Find the median, which is Q2.
   • Find Q1, which is the median of the lower half of the dataset (excluding Q2)
   • Find Q3, which is the median of the upper half of the dataset (excluding Q2)
2. Calculate IQR:
   • IQR is the range between the Q1 and Q3.
   • $IQR=Q3-Q1$

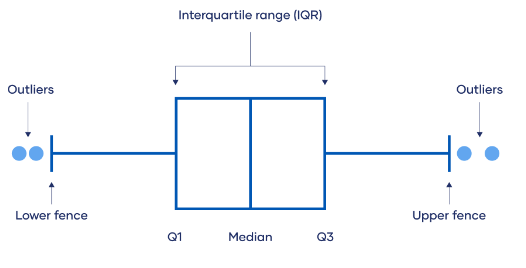
Image Source: https://www.scribbr.com/statistics/interquartile-range/

Box-and-whisker plots visualises the distribution of data, where the box represents the interquartile range, and the “whiskers” extend to the minimum and maximum values between the lower and upper fence (usually $\pm$ 1.5 times the IQR) to identify potential outliers.

Definition: A measure of how spread out the values in a dataset are from the mean.

Formula: $Var=\frac{\sum _{i=1}^n(X_i-\overline{X}{)}^2}{n}$

• $Var$: The variance.
• $n$: The total number of observations.
• $\overline{X}$: The mean.
• $X_i$: Represents each individual value in the dataset.
• $\sum$ denotes the sum of the squared differences between each value and the mean.

Definition: A measure of how spread out the values in a dataset are from the mean.

Formula: $SD=\sqrt{Var}$

• $SD$: The standard Deviation
• $Var$: Variance

• To ensure positivity: Squaring the differences ensures that all values are positive. Without squaring them, positive and negative differences might cancel each other out, resulting in a net difference of zero.
• Exaggerate larger deviations: Larger deviations are often considered more important in assessing the spread or variability of a dataset.

$SD$ is more applicable because it uses the same units as the original statistics, making it easier to interpret. For example, if the measurements are in metres you want a measure of spread to be in metres, not in metres squared.

Stating $SD$ in relation to the mean is important because it provides information about the spread in the context of the average. Expressing it in relation to the mean helps quantify how spread out or concentrated the data values are around the average.

Definition: A measure of the average absolute difference between each data point in a dataset and the mean of that dataset.

Formula: $MAD=\frac{\sum _{i=1}^n|X_i-\overline{X}|}{n}$

• $MAD$: The mean absolute deviation.
• $n$: The total number of observations.
• $\overline{X}$: The mean.
• $X_i$: Represents each individual value in the population.
• $\sum$ denotes the sum of the squared differences between each value and the mean.

No, $SD$ must be equals or more than $MAD$.

Central Tendencies will be affected. However, dispersion measures will not be affected.

Both central tendencies and dispersion measures will be affected.

Image Source: https://www.scribbr.com/statistics/skewness/

• Right Skewed: Mean is greater than median. The right left tail pulls the mean in that direction.
• Left Skewed: Mean is less than median. The longer left tail pulls the mean in that direction.
• No Skew: Mean and median are approximately equal if the distribution is symmetrical.

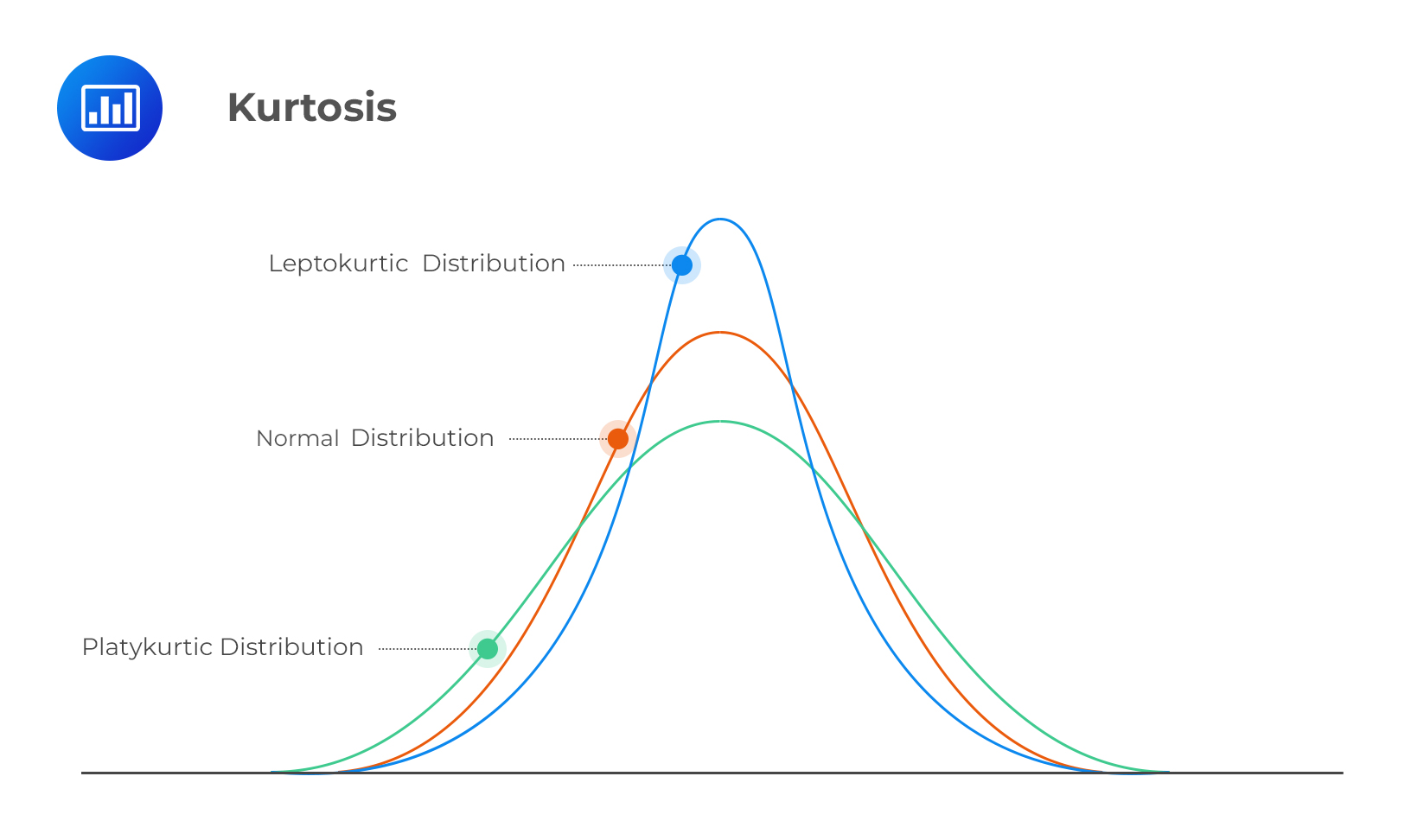
Image Source: https://analystprep.com/cfa-level-1-exam/quantitative-methods/kurtosis-and-skewness-types-of-distributions/

• High Kurtosis (Leptokurtic): Characterised by a higher peak and heavier tails compared to a normal distribution. This indicates that the data has more extreme values (outliers) and is more concentrated around the mean.
• Low kurtosis (Platykurtic): Characterised by a flatter peak and lighter tails than a normal distribution. This suggests that the data has fewer extreme values, and the values are more spread out from the mean.