Functions

1. Define functions.

A function in mathematics is a relation between a set of inputs and a set of outputs, where each input is related to exactly one output.

2. Provide the another term for inputs and outputs of the function.

The set of inputs is called the domain of the function and the set of outputs is called the co-domain of the function.

3. Can a function have two different inputs that would return the same output? Provide an example.

Yes, a function that returns the square will provide the same output.

4. Explain the difference between equation and functions.

Equation is a statement of equivalence.
Function is a relationship between variables.

5. Explain the function notation

f (x)

The notation

f (x)

is used to represent the output of the function

f

applied to the input

x

6. Explain the phrase:

y

is a function of

x

y = y (x)

and

y

varies according to whatever value

x

takes on.

7. Every function is a relation but not every relation is a function. Explain the sentence.

Every Function is a Relation: All functions are relations because they inherently establish a connection between elements of sets. Functions are a specific type of relation with the added constraint of unique output values for each input.

Not Every Relation is a Function: Not all relations are functions because they can have multiple outputs for a single input, making them more general than functions.

8. Provide the formula to represent a function

(f)

that squares its input

(x)

$f (x) = x^{2}$

9. Provide the visual representation of domain, codomain and range.

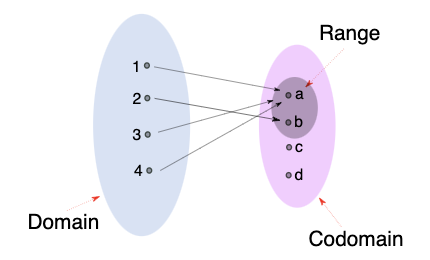
Image Source: https://the-learning-machine.com/article/math/relations

10. Provide the formula to represent the cost of a product as a function of the quantity purchased:

cost(quantity) = price x quantity

11. Explain the difference between range and co-domain. Use

f (x) = x^{2}

to explain the difference.

Codomain: The set of all possible outputs that the function could produce, but may not actually produce.
- For the function $f (x) = x^{2}$ , where the codomain is the set of real numbers ℝ. In this case, the codomain encompasses all real numbers, but not all real numbers are necessarily output values of the function.
Range: The set of all possible output values that the function can produce.
- For the function $f (x) = x^{2}$ , if the domain is specified as all real numbers (ℝ), the range is a subset of ℝ, consisting of all non-negative real numbers (i.e., the set of real numbers greater than or equal to zero).

12. Provide the formula to represent a function (f) that outputs the remaining filling for the dumping (d) given that each dumpling requires 20g of filling starting with 1500g of fillings.

f (d) = 1500 - 20 d

13. Given the equation

4 a + 7 b = - 52

, write a formula for

f (b)

in terms of

b

Essentially express $a$ as a function of $b$ by solving for $a$ .
$f (b) = \frac{- 52 - 7 b}{4}$

14. Explain absolute value function and provide the standard form.

The absolute value of a number is its distance from zero on the number line, and it is always non-negative. This means that the absolute value of any number is the same as the number itself,
Standard Form: $f (x) = | x |$

15. Solve this equation

∣ x - 3 ∣= 5.

$x - 3 = 5, x = 8$
$- (x - 3) = 5, x = - 2$

16. Explain piecewise functions.

Piecewise functions also known as hybrid functions or step functions, is a function that can be defined by multiple sub-functions, where each sub-function applies to different interval in the domain.
Example:

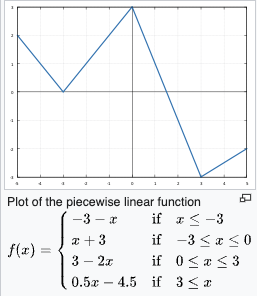
Image Source: https://en.m.wikipedia.org/wiki/File:Piecewise_linear_function_gnuplot.svg

Last updated on 19 Nov 2023